Elektrische Schwingungen
Erstellen Sie einen Kurzvortrag von maximal 5 Minuten Länge, in dem Sie zu einem der folgenden Themen einen Vortrag mit Präsentation halten.
Achtung: Es müssen keine harmonischen Schwingungen sein, die behandelt werden.
Kontexte als Vorträge
Mögliche Themen
- Steuerung von Maschinen (z.B. Antriebe, Servos) per PWM
- Steuerung von Drehstrommotoren
- E-Gitarre
- Lautsprecher
- Mikrofon
- IR-Fernsteuerung (bevor und nachdem die Daten/Impulse übertragen wurden)
- Eigenes Thema bei dem el. Schwingungen eine relevante Rolle spielen
- Horn und Hupe
Anforderungen an den Vortrag
- Erläuterung des Beispiels/Kontext
- Jede Folie mindestens 1 Bild
- Keine Sätze außer Zitate
- physikalisch korrekte Darstellung der Schwingung als Graph
- technische bzw. praktische Nutzung
- Besonders interessante/extreme Nutzungen
Roadmap
- Freitag (heute): Demo am Beispiel Dimmen von Dioden, Festlegung des Themas
- Montag: Erster Entwurf Vortrag, Arbeitsphase, Abgabe bei mir
- Dienstag: Vortrag der Top 3 + x
Dimmen von Licht emittierenden Dioden (LEDs)
Beispielvortrag als Screencast
Der Schwingkreis
Randbemerkung: Hier wird aus Sparsamkeitsgründen oft von elektrischen Schwingungen gesprochen. Die Fachwelt benennt diese aber oft als elektromagnetische Schwingung.
Die Phasen des Schwingkreises sollen auf Basis des Lehrbuches (LBS. 214 ff) herausgearbeitet und im Hefter festgehalten werden.
Zur illustration noch eine Animation zum Auf- und Abbau der elektrischen oder magnetischen Felder:

https://www.ulfkonrad.de/physik/12-13/2-semester/schwingungen-2/schwingkreis-elektrisch
Experiment: Schwingkreis
- Erstellen Sie einen Schaltplan vom Aufbau
- Notieren Sie Ihre Beobachtungen in Stichpunkten
- Skizzieren Sie das Messergebnis des Oszilloskops
- Formulieren Sie einen zusammenhängenden Text, der die Messergebnisse, insbesondere das Entstehen der elektrischen Schwingung erklärt. Verwenden Sie dabei insbesondere den Energiebegriff und die passenden Formeln.
Failsave

Der "ideale" ungedämpfte Schwingkreis
Musterlösung 1 - der naive Ansatz
\( E_{el} = {1 \over 2} C U^2 \)
\( E_{mag} = {1 \over 2} L I^2$$ \)
Leider ein Irrweg...
...aber nette Gleichungen.
Herleitung auf Uni-Niveau
Musterlösung 2 - so wird es etwas
Aus
\( U_{L} = L {d I \over dt} = L \dot{I} \)
und
\( U_{C} = {Q \over C} \)
und
\( U_C = -U_L \)
folgt:
\( -{1 \over C} Q = L \dot{I} \)
wobei
\( I = \dot{Q} \)
und damit
\( -{1 \over C} Q = L \ddot{Q} \)
Hier verlangt Berlin nicht sonderlich viel und wir sind über das lineare Kraftgesetz für harmonische Schwingungen "hinweg gegangen"...
analog zu: \( m \ddot{y} = -k y \) mit \( T = 2 \pi \sqrt{m \over k}\)
wird für \( L \ddot{Q} = -{1 \over C} Q \) bestimmt:
\( T = 2 \pi \sqrt{L C} \) und \( T = {1 \over f }\)
Eigenfrequenz
$$ f_0 = {1 \over {2 \pi \sqrt{LC}} }$$
aka Thomson'sche Schwingungsgleichung
Mal wieder etwas rechnen
https://www.leifiphysik.de/elektrizitaetslehre/elektromagnetische-schwingungen/aufgabe/thomsonsche-schwingungsgleichung
SalzH: Vertiefung / Wiederholung
https://www.leifiphysik.de/elektrizitaetslehre/elektromagnetische-schwingungen/grundwissen/elektromagnetischer-schwingkreis-ungedaempft
Die Animation Abb2. simuliert verschiedene Schwingungen verschiedener physikalischer Größen unter der Veränderung von Kapazität und Induktivität.
- Beschäftigen Sie sich mit der Animation und verändern Sie alle möglichen Parameter
- Beschreiben Sie die Unterschiede zwischen E(t)-Schwingungen und U(t)-Schwingungen.
- Erläutern Sie, weshalb die Energie-Schwingungen eine andere Form haben, als die Ladungs-, Stromstärke- oder Spannungsschwingungen.
- Begründen Sie, weshalb die I(t)-Amplitude sich verändert, wenn Sie die Kapazität variieren.
- Begründen Sie, weshalb sich die Amplitude im I(t)-Diagramm aber nicht im U(t)-Diagramm ändert, wenn man die Induktivität variiert.
Weisen Sie Ihre Arbeitsergebnisse (Texte) per E-Mail an mich nach.
Der weniger ideale Ausblick: Einfach genial!
Meißnersche Rückkopplungsschaltung
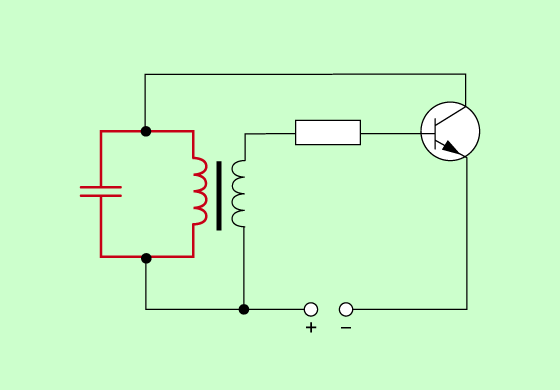
https://www.lernhelfer.de/schuelerlexikon/physik/artikel/meissnersche-rueckkopplungsschaltung
Transistor


Basis - Collector - Emitter
Werden alle Transistoren in sämtlichen bislang hergestellten Schaltkreisen wie Arbeitsspeicher, Prozessoren usw. zusammengezählt, ist der Transistor inzwischen diejenige technische Funktionseinheit, die von der Menschheit in den höchsten Gesamtstückzahlen produziert wurde und wird. Moderne integrierte Schaltungen, wie die in Personal Computern eingesetzten Mikroprozessoren, bestehen aus vielen Millionen bis Milliarden Transistoren, so besitzt die 2022 veröffentlichte Grafikkarte RTX 4090 76,3 Milliarden Transistoren.
https://de.wikipedia.org/wiki/Transistor
Aufgaben
- Formulieren Sie einen Vorschlag, wie Sie der (starken) Dämpfung eines realen Schwingkreises entgegenwirken können.
- Entwerfen Sie ein Schaltbild, dass in der Meßnerschen Schaltung an den geeigneten Stellen Messgeräte ergänzt.
- Stellen Sie eine Tabelle auf, die in 1/8T-Schritten des Schwingkreises vor allem die Rückkopplung erklärt. Als Spaltenüberschriften wählen Sie die Messwerte aus der vorangegangenen Aufgabe.
- Begründen Sie, weshalb diese Schaltung zwar dauerhafte harmonische Schwingungen erzeugt, aber nicht von einer stabilen Frequenz ausgegangen werden kann.
Finale
Plan A
Plan B
- Vertiefung: Wünsche
- Vertiefung: Curriculum
- Vertiefung: Harmonische Schwingungen, Kräfteansatz
![]()

![]()
